index
Note (Extra Reading)
3Blue1Brown’s linear algebra series for Linear combinations, span, and basis vectors. Start with this episode:
Vector Equation
Given vectors {a1,a2,…,an,b} in Rm, determine if b is a linear combination of a1,…,an
This is equivalent to solving the vector equation:
x1a1+⋯+xnan=b
Which is the same as checking if the augmented matrix
[a1a2⋯an∣b]
has a solution (via EROS).
Review
- b is a linear combination of a1,…,an
- The vector equation x1a1+⋯+xnan=b has a solution.
- We answer this by reducing the augmented matrix to (reduced) echelon form.
Example
Suppose
a1=0248,a2=0248,a3=6−11−1,a4=061026,b=1241323
We want x1a1+x2a2+x3a3+x4a4=b
Augmented matrix:
024802486−11−1061026∣∣∣∣1241323
Row-reduce (EROS) to:
1000100001000010∣∣∣∣3/221/20
The solution is a one-dimensional general solution
x1=23−s,x2=s,x3=2,x4=21
From Vectors to Span
- Linear combinations involve adding vectors.
- This is how we visualize addition of vectors:
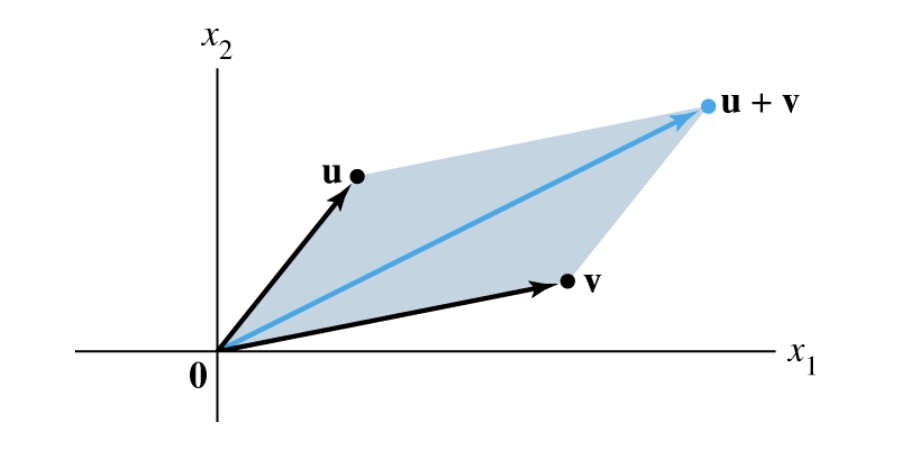 Figure 1: Vector addition visualization
Figure 1: Vector addition visualization
We often have to consider all possible linear combinations of a given collection of vectors.
In solving systems with infinitely many solutions, the solutions involve
s−11000+t−π0−e10
for any choices of s,t
Span
Definition (Span)
Given {v1,v2,…,vk}, the set of all linear combinations:
c1v1+⋯+ckvk,ci∈Ris called the span of {v1,…,vk}, denoted
Span{v1,…,vk}
If k=1 so there’s only one vector, then Span{v} is just all vectors that are multiples of v
i.e., {cv∣c∈R} (a line through 0 and v).
Example
The collection of vectors
s−11000+t−π0−e10
for all possible choices of s,t form the span
Span⎩⎨⎧−11000,−π0−e10⎭⎬⎫
Visualization
Picture this span when k=1,2:
- k=1: span is a line through 0 and v → Span{v}={cv}
- k=2: span is Span{u,v}={c1u+c2v} (Figure 2)
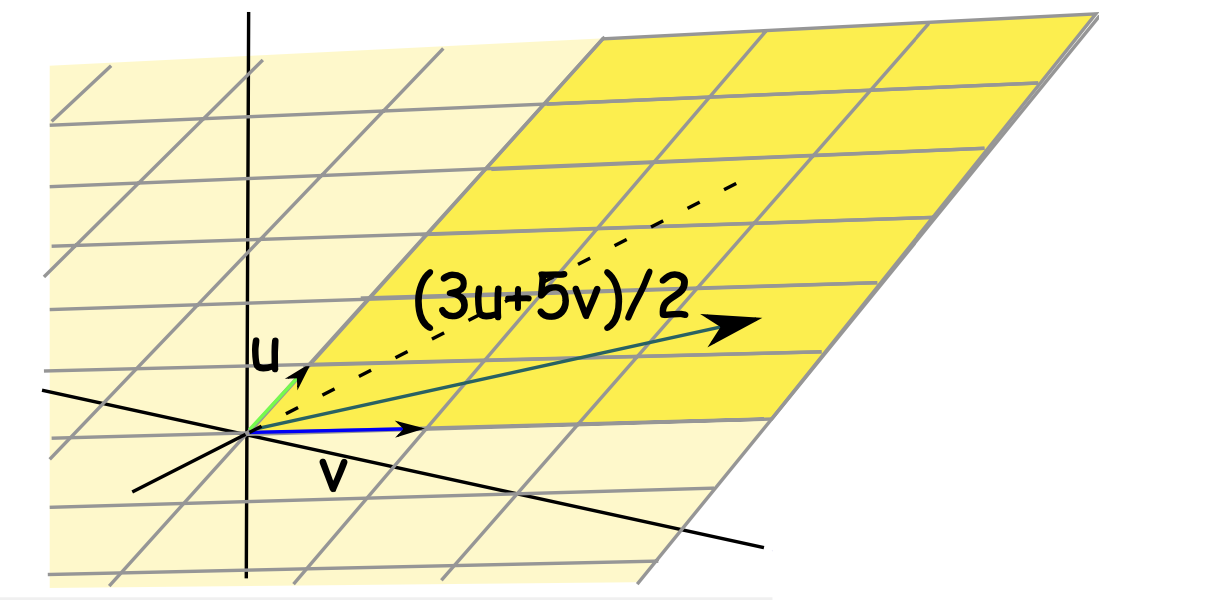 Figure 2: when k=2, Span = entire plane, ci>0 highlighted
Figure 2: when k=2, Span = entire plane, ci>0 highlighted
Spanning Solutions
Back to example above:
024802486−11−10610261241323⇒10001000010000103/221/20
General solution was
x1=23−t,x2=t,x3=2,x4=21
We can rewrite this as
c1c2c3c4=3/2021/2+t−1100
So we can think of the set of all solutions as
3/2021/2+Span⎩⎨⎧−1100⎭⎬⎫
where p=3/2021/2 is a point, and d=−1100 is the direction.
We can picture the solution as a line in the direction of the second vector, going through the point given by the first vector (In R4)
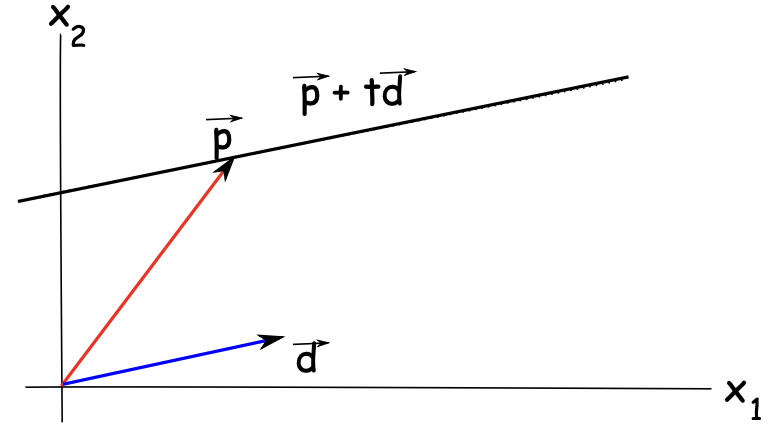 *Figure 3: Visualization of spanning solutoin
*Figure 3: Visualization of spanning solutoin
 Figure 1: Vector addition visualization
Figure 1: Vector addition visualization Figure 2: when , Span = entire plane, highlighted
Figure 2: when , Span = entire plane, highlighted *Figure 3: Visualization of spanning solutoin
*Figure 3: Visualization of spanning solutoin